Marginal Exposure represents the effect of each specific contract on aggregated Expected Exposure of the portfolio. If portfolio includes only one contract, then Marginal Exposure of the contract equals to portfolio exposure.
The aim is to find allocations of that reflect
trade contribution to the overall risk for each period
and sum up to the counterparty level
.
1. No netting
“No netting” here means that contracts are fully independent and we cannot take net value. in this case equals to the sum of the individual components and hence the
will equal the
.
If no netting is assumed, then Total Exposure of portfolio is just a summation of individual positive exposures. The logic is straightforward: Marginal Exposure for given contract at certain period of time is computed as average of positive simulated exposures for each specific contract. Now assume we have 1000 of simulations of exposures. Marginal exposure in this case should be computed as expected value across all simulations.
, where
is index function.
2. Netting
Similar formula can be applied for portfolio with netting:
,
where is index function.
Difference with previous formula is that average is computed only with positive values if netting set
was positive. If netting is assumed, then Marginal Exposure for given contract at certain period of time is computed as average of: positive simulated exposures if total value of the set to which this contract belongs is positive; 0 if value of this contract in this simulation is zero or negative.
Example: 2 contract, 2 simulations, 5 periods
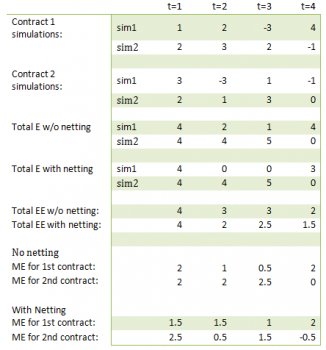
In the example above in the second period we compute ME for the first contract as (2*(0>0)+3*(4>0))/2=(0+3)/2=1.5
Please notice that sum of marginal effects equals to total effect.
Notations:
— contract index;
— simulation index;
— period index;
— simulated exposure for contract
at period
where
is number of simulation;
— expected exposure for contract
at period
;
— total exposure in simulation
at period
;
— total expected exposure at period
;
— marginal exposure for contract
at period
;
— number of simulations.