The delta equivalents of a position describe the response of a position/portfolio to a change in the market data.

Delta equivalent is the derivative of the Present Value with respect to a given risk factor, multiplied by the value (price) of that particular risk factor:


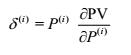
Delta equivalent value is based on:

For equities, currencies and commodities: % price change in the underlying price series;

In the case of interest rates: % price changes in the price of the corresponding zero-coupon bond for each key rate point on the discount curve.

 

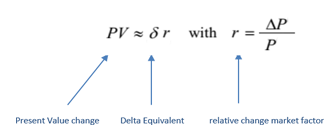
Present Value response can be computed as:

Delta Equivalents are additive, i.e. you can add values to get effect on entire portfolio.

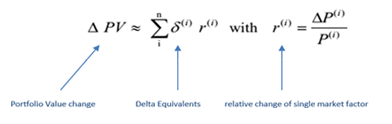
Note: Delta Equivalent is an approximation.

Examples:

If the value of market factor changes by 100%, then Present Value of the position would change by USD.

If the values of market factors A and B change by 1% and 2%, respectively, then Present Value of the position would change by 0.01* + 0.02* USD.

If the value of 4-year zero-coupon USD Goverment bond increases by 1% in absolute amount, then 5-year bond’s price (which has USD Government bond as underlying risk factor) would change approximately by 0.01*.

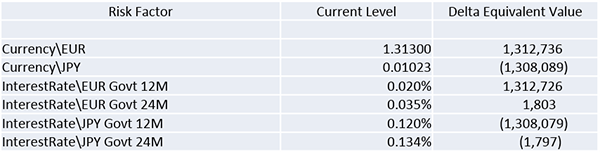
Example below shows that 1% decrease of EUR/USD exchange rate would change the portfolio value by 1,312,736/0.01=13,127 USD.

In case only yield change is known, we can convert price sensitivities to yield sensitivities: ,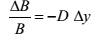
where B is bond price, D – duration, y – yield. Thus:

If yield for InterestRate\EUR Govt 24M (in the table above) increases by 0.01% (1bp), then PV of the portfolio would change by -2*0.0001*1,312,726=262 USD.

If the yield of the 4-year zero-coupon USD Goverment bond decreases by 25bp, then the 5-year bond’s yield would change approximately by -4*0.0025*(USD Govt 4Y).

---

See also: help.riskmetrics.com
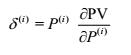
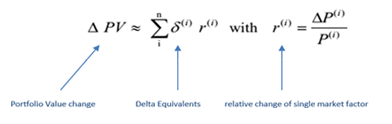
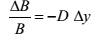